北京電影學(xué)院發(fā)了一篇滿是數(shù)學(xué)公式的計算機頂會論文，并開源了其代碼
2019-07-29 15:06:11 知乎這個方程，對于做流體動力學(xué)的讀者一定不陌生，數(shù)十年來科學(xué)家們?yōu)榱擞嬎銠C翼升力，已將其研究了百千萬遍。
然而基于影視制作的特別需求，影視科技工作者們對這個方程的求解提出了新的需求：
我們需要能夠處理更大的時間步長以及不損失精度細節(jié)！！這兩者本來是魚與熊掌不可兼得，這就等于是在說：
于是伴隨著特效應(yīng)用的發(fā)展，十數(shù)年來，計算機圖形學(xué)的科技工作者為了戰(zhàn)勝這個問題不斷地添磚加瓦，這里面比如就有大家耳熟能詳?shù)目蒲袑W(xué)府：
斯坦福的科學(xué)家就曾經(jīng)提出過使用渦旋力來增加流體的細節(jié):
他們的論文研究的算法，甚至直接和工業(yè)光魔合作，使用在當年星球大戰(zhàn)特效鏡頭的制作上
還有很多科研機構(gòu)也是不斷地在算法上推陳出新，甚至像迪士尼這樣家里有礦的影視工作室還親自上陣，不斷地革新著美利堅的影視制作技術(shù)，帶動起了好萊塢產(chǎn)-研結(jié)合的影視工具生態(tài)。
而不管是由工業(yè)光魔發(fā)表的用來補充煙火高精度細節(jié)的算法
還是來源于迪士尼研究院-ETH Zurich的小波湍流論文
都是不斷在嘗試攻克一個令人頭疼的問題：如何在使用高效穩(wěn)定的流體特效仿真算法前提下，盡可能地保證流體運動的細節(jié)，這最終落在了對于N-S方程中的對流部分的求解上。
在圖形學(xué)特別是影視特效制作軟件中，為了追求大時間步長的穩(wěn)定性，對流方程的求解多采用半拉格朗日方法或其變種。這類方法雖然高效穩(wěn)定，但有它最大的問題：數(shù)值粘性。
所謂數(shù)值粘性，顧名思義，就是物理系統(tǒng)中本不存在的粘性，是被人類設(shè)計的數(shù)值算法在求解方程的過程中帶入系統(tǒng)的，與真實的物理事實相左。 我們先領(lǐng)略一下“數(shù)值粘性” 會帶來的問題：
流體的運動更為復(fù)雜，計算機算法保持清晰（守恒）的能力，就顯得尤為重要。
為了對抗這種過度平滑，科技工作者們提出了混合的粒子-網(wǎng)格方法，然而這類方法存在著計算速度慢，計算結(jié)果差強人意的缺陷：往往由于粒子的非連續(xù)性，流體的湍流運動會在粒子間拉出空隙，最終在視覺上產(chǎn)生噪聲：
為了以極高的清晰度來對流流體中的物質(zhì)場我們給出了以下觀察：
傳統(tǒng)的對流算法直接作用于流體空間中的“物理量”，數(shù)值粘性于是會累加在“物理量”上，并最終造成“物理量”的模糊。
如果能構(gòu)造出一個映射，使得流體場中的每一個空間點在任何時候都能知道自己初始時刻的位置并去初始時刻訪問物理量的信息我們就能夠避免在對流的過程中累加“數(shù)值粘性”。
這個哲學(xué)像極了愛情：一切若只如初見，是多么的美好。
這個方法從求解的根本思路上跳出了傳統(tǒng)對流方程求解方式：
以往的方法對流“物理量”
我們的方法對流“空間”本身。
為此，我們定義了一個映射，這個映射的目的是將空間中的點映射回它初始時刻的位置
這個初始位置，滿足如下的數(shù)學(xué)關(guān)系。稱之為后向映射。
在這個基礎(chǔ)上，我們就有機會將原本的對流方程拆為空間的對流和物理量的重構(gòu)兩個部分
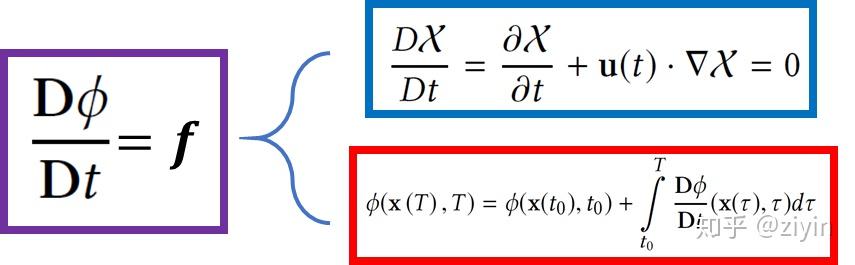
為了便于重構(gòu)物理量時對于積分項的計算，我們提出了整個算法中最至關(guān)重要的部分：前向映射。并給出了前向映射的演化方程:
有了前向映射。積分的過程變?yōu)榱搜莼奂拥倪^程（大大減少了計算量）
好了，小編保證，不會再有數(shù)學(xué)公式了！
我們將我們發(fā)明的這樣層級前-后向映射來求解對流方程的形式稱之為“n層級雙向跡徑映射對流求解法”。
Bi-Directional Characteristic Mapping of Convective Quantaties of Level n BiMocq.
雖然不打算在這里展開討論，這樣的做法使得在保持流體物理量守恒的同時還保證計算極為高效以及并行友好，大大地區(qū)別于混合的粒子-網(wǎng)格算法。我們粗暴實現(xiàn)的GPU代碼可以對比相應(yīng)的CPU的并發(fā)式代碼加速50倍。
那么，BiMocq好處都有啥？
我們首先是對比了一個數(shù)學(xué)上有比較確定的答案的問題，“泰勒渦旋”：
兩個初始狀態(tài)如下的渦旋，在無粘的環(huán)境中，能量守恒的數(shù)值積分應(yīng)該可以將其分開
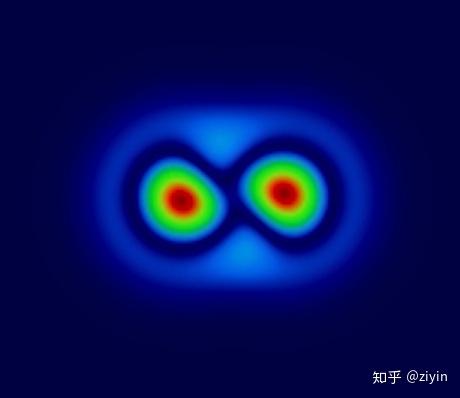
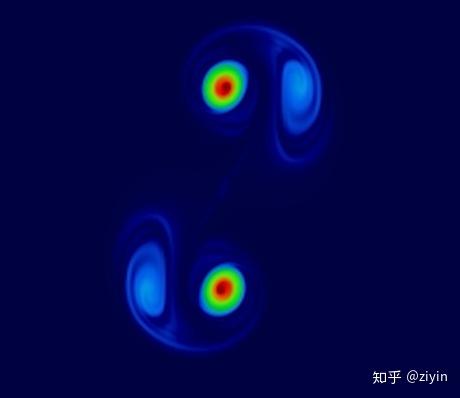
對此，我們實現(xiàn)并且對比了幾乎所有主流使用的，先前發(fā)表于SIGGRAPH論文的算法，并驗證了我們的算法在能量守恒上的優(yōu)越性
以及難以用Eulerian方法解算的leapfrogging vortex：
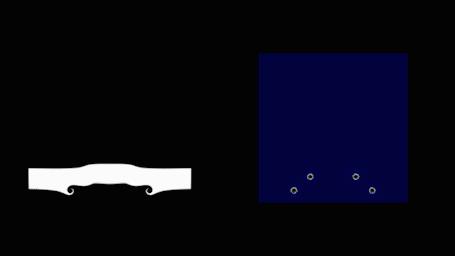
以往的算法無法保證煙霧運動時的清晰形狀導(dǎo)致了其在之后的效果計算中損失了煙霧的
湍流細節(jié)，那些更能體現(xiàn)煙霧真實感的卷曲細節(jié)。
大自然是最好的藝術(shù)家，我們想做的，僅僅是用程序在計算機中再現(xiàn)它的美。為此，我們用我們的數(shù)值算法在計算機中再現(xiàn)了如下場景，渦環(huán)相撞實驗。
這樣的現(xiàn)象以往的數(shù)值算法存在數(shù)值粘性就根本不可能重現(xiàn)出來
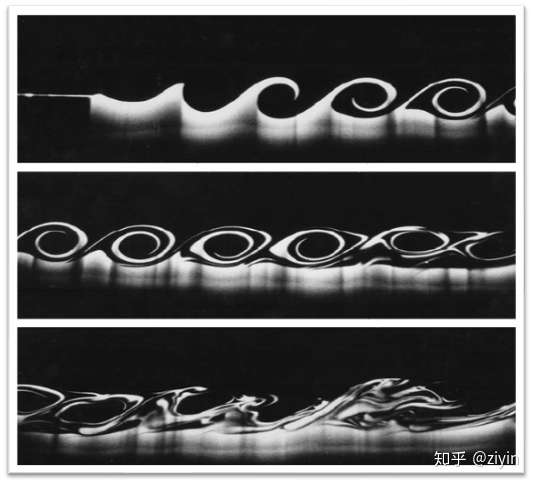
這種現(xiàn)象被稱為開爾文-亥姆霍茲-瑞利-泰勒不穩(wěn)定性(Kelvin–Helmholtz-Rayleigh-Taylor instability)，這種現(xiàn)象通常由于兩種不同密度的流體在交界面處由于擾動而產(chǎn)生的不穩(wěn)定現(xiàn)象。
同樣，我們使用我們的算法對這個現(xiàn)象進行了近似的模擬。我們可以看到由于密度本身的對流會對整個流場產(chǎn)生影響，對比以往的數(shù)值算法，在同等分辨率下由于我們的算法對密度對流有著更準確的估計，因此我們也能更準確地模擬這種不穩(wěn)定性帶來的渦結(jié)構(gòu)。
EETOP 官方微信
創(chuàng)芯大講堂 在線教育
半導(dǎo)體創(chuàng)芯網(wǎng) 快訊
相關(guān)文章
